José Anastácio da Cunha (Lisboa, 1744 – 1 de janeiro de 1787)
Palavras-chave: matemático, livre-pensador, poeta.
DOI: https://doi.org/10.58277/KNIH4583
José Anastácio da Cunha foi um dos primeiros professores da Faculdade de Matemática criada na reforma pombalina da Universidade de Coimbra. A sua obra, publicada postumamente, revela uma preocupação invulgar para a época com o rigor lógico, e particularmente com definições precisas e gerais. Algumas das suas definições são frequentemente vistas como precursoras de soluções adotadas a partir do século XIX.
José Anastácio da Cunha nasceu numa família modesta, mas não sem algumas ligações importantes. O seu pai, Lourenço da Cunha, foi um pintor conceituado, autor de cenários teatrais e de algumas pinturas em igrejas e capelas, e foi juiz da Irmandade de São Lucas (corporação de pintores e artistas). A sua mãe, Jacinta Inês, foi criada na casa do tesoureiro-mor do reino.
Com o pai, Anastácio da Cunha aprendeu desenho, incluindo perspetiva e talvez um pouco de geometria, mas fez os estudos formais na escola da Congregação do Oratório no Convento das Necessidades, à parte uma passagem de dois anos pela Universidade de Coimbra para cursar Leis, sem seguimento.
Em 1764 foi nomeado primeiro-tenente do Regimento de Artilharia do Porto, aquartelado em Valença. Aí travou amizade com diversos oficiais estrangeiros ao serviço do exército português. Aprendeu inglês e possivelmente alemão (em Lisboa já tinha aprendido latim e francês). O convívio com estrangeiros, muitos deles heréticos do ponto de vista católico da época, influenciou profundamente Anastácio da Cunha, que se tornou um livre-pensador. Leu e traduziu autores como Pope, Voltaire e Shakespeare, além de compor poesia própria. Um dos estrangeiros com quem conviveu foi o capitão inglês Richard Muller, filho de John Muller, professor da Royal Military Academy de Woolwich e autor de vários compêndios de matemática, artilharia e fortificação. Muller e mais tarde o coronel escocês James Ferrier, deram a Anastácio da Cunha acesso a alguma da mais importante bibliografia científica britânica, incluindo os Principia Mathematica e outras obras de Newton. As primeiras produções científicas conhecidas de Anastácio da Cunha datam desta fase e relacionam-se com aplicações militares: o Ensaio sobre as Minas, não datado (mas anterior a março de 1768) e a Carta Físico-Matemática sobre a Teórica da Pólvora em Geral e a determinação do melhor comprimento das peças em particular, de 1769. No entanto, segundo declarações posteriores à Inquisição, começou também em 1766 a trabalhar numa obra com «a Baze de toda a Mathematica»; é provável que essa obra corresponda à Arithmetica Universal de que se sabe que existia uma versão em 1771.
Em 1773 José Anastácio da Cunha foi nomeado pelo marquês de Pombal lente de Geometria na Universidade de Coimbra, completando o quadro docente da Faculdade de Matemática (FM) criada na reforma pombalina da instituição. No ano anterior tinham sido nomeados os outros três lentes: os italianos Miguel Franzini e Miguel António Ciera e o ex-jesuíta português José Monteiro da Rocha. Geometria era o título da cadeira do primeiro ano, que compreendia aritmética, geometria (sintética) e trigonometria plana. Em Coimbra, Anastácio da Cunha parece ter direcionado a sua atenção mais para a matemática pura. Em abril de 1776, propôs na Congregação da FM, sem sucesso, a adoção duns Elementos de Geometria que tinha composto “por metodo mais breve e mais facil”.
Ainda em Coimbra compôs um texto em inglês: Logarithms & powers, datado de maio de 1778, uma investigação sobre um tema que lhe era caro — a maneira correta de definir potências e logaritmos, de forma a abarcar todos os casos dos expoentes (naturais, fracionários e irracionais) logo na definição. No século XVIII as potências eram definidas como multiplicações repetidas, o que só faz sentido com expoentes naturais; potências de expoentes fracionários e irracionais eram calculadas utilizando expressões cuja validade estava demonstrada apenas para expoentes naturais. Uma situação semelhante acontecia com as definições de logaritmos. Anastácio da Cunha era extremamente crítico deste tipo de abordagem, em que as definições não cobrem todos os casos. A sua proposta naquele texto consistia em definir os logaritmos a partir de uma equação funcional (a soma dos logaritmos é igual ao logaritmo do produto) e depois definir e estudar a exponencial como função inversa do logaritmo. Tecnicamente recorria à série de potências da exponencial, depois de verificar que a sua função inversa verifica a equação funcional dos logaritmos.
Em Coimbra, travou amizade com alguns jovens estudantes nobres que viriam a fazer parte duma elite política e cultural, particularmente na regência de D. João. Entre eles contavam‑se D. Rodrigo de Sousa Coutinho (futuro diplomata e secretário de estado em várias pastas), D. Domingos de Sousa Coutinho (futuro diplomata) e D. José Maria de Sousa (também futuro diplomata, o mais conhecido dos morgados de Mateus; é célebre a sua edição dos Lusíadas). Quanto aos seus colegas da FM, parece ter tido boas relações com Ciera, mas um pouco mais tensas com Franzini e Monteiro da Rocha, que viriam a ter posições de maior influência (o primeiro foi mestre dos príncipes D. José e D. João e o segundo Vice-Reitor da Universidade e figura importante na Academia das Ciências de Lisboa).
Em julho de 1778, cerca de um ano e meio após a morte de D. José e o afastamento do marquês de Pombal (isto é, em plena Viradeira), José Anastácio da Cunha foi preso pela Inquisição. Considerado culpado de heresia e apostasia, por ter caído nos erros do deísmo, tolerantismo e indiferentismo, foi condenado a confisco de todos os seus bens, três anos de reclusão na Congregação do Oratório em Lisboa (Casa das Necessidades), quatro anos de degredo em Évora e proibição de voltar a entrar em Coimbra ou Valença. Posteriormente foi-lhe comutado um ano de reclusão e perdoado o degredo em Évora.
Durante os dois anos de reclusão Anastácio da Cunha manteve atividade científica. Escreveu pelo menos um texto sobre balística e uma versão dos Princípios do Cálculo Fluxionário, sobre outro dos seus temas importantes: a fundamentação do cálculo diferencial (a que chamava “fluxionário”, usando terminologia newtoniana). Ao longo do século XVIII houve muitas discussões sobre como fundamentar o cálculo diferencial; uma das duas respostas mais importantes recorria a quantidades infinitamente pequenas ou infinitésimos (Leibniz) e a outra argumentava com limites (Newton e d’Alembert); mas as quantidades infinitamente pequenas não pareciam bem definidas (ora se comportavam como zeros, ora não) e os argumentos com limites eram vagos. A proposta de Anastácio da Cunha consistia resumidamente em substituir as quantidades infinitésimas por variáveis infinitésimas — variáveis que podiam tomar valores arbitrariamente pequenos, mas não infinitamente pequenos — e em definir fluxão de φx como a grandeza dφx que, supondo dx infinitésimo, fizer dφx/dx constante e
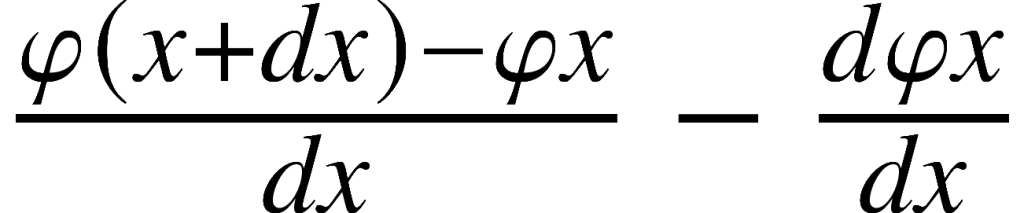
infinitésimo ou zero. Esta definição foi descrita por diversos historiadores desde a década de 1970 como a primeira definição analítica rigorosa de diferencial.
Nos finais de 1779, foi fundada a Academia das Ciências de Lisboa, instalada precisamente no edifício oratoriano das Necessidades onde Anastácio da Cunha estava recluso. Este nunca pertenceu à Academia, mas foi consultado, através do padre oratoriano Teodoro de Almeida, seu amigo e diretor espiritual, e também académico fundador, a propósito de problemas de matemática a propor pela Academia.
Depois de libertado, Anastácio da Cunha tentou publicar, por subscrição, uns Ensaios Mathematicos em dois volumes, que seriam uma compilação de estudos seus, revistos, sobre temas de matemática pura (geometria, “aritmética universal”, cálculo fluxionário) e mecânica. O anúncio na Gazeta de Lisboa (15/6/1781) resumia a preocupação científica fundamental de Anastácio da Cunha: “remover, e destruir muitas das grandes difficuldades, que ainda hoje fazem assás precaria a evidencia de algumas partes da Mathematica […] conservar a evidencia, rigor, e elegancia dos Geometras Gregos”. Contudo, o número de subscritores foi insuficiente para a publicação.
Por essa altura, mas em data que não é possível precisar, o intendente-geral da Polícia, Pina Manique, convidou José Anastácio da Cunha para regente (ou inspetor) dos estudos e substituto das cadeiras de matemática no colégio da Casa Pia de Lisboa, recém-criada. Nessa qualidade, Anastácio da Cunha elaborou o Plano de Estudos do colégio. Alguns dos seus alunos na Casa Pia viriam a ter carreiras académicas: Manuel Pedro de Melo foi professor na FM de Coimbra, tendo ganhado em 1806 um prémio da Academia Real de Copenhaga; Tristão Álvares da Costa Silveira foi professor na Academia dos Guardas-Marinhas e depois na FM de Coimbra. Também com o patrocínio de Pina Manique começaram a imprimir-se os seus Principios Mathematicos, provavelmente em 1782. Segundo João Manuel d’Abreu, à medida que eram impressos, os primeiros cadernos deste livro eram utilizados no ensino no colégio, sob supervisão de Anastácio da Cunha. O lugar de Anastácio da Cunha na Casa Pia não durou muito tempo, mas também não se sabe exatamente quando terminou. Em 1783, ainda constava na folha de vencimentos da Casa Pia, mas em 1785 queixava-se de terem destruído a obra do intendente.
Nos dois ou três últimos anos da sua vida José Anastácio da Cunha, para além de não ter emprego, sofreu de problemas de saúde, tendo de recorrer à ajuda de amigos. Continuou a trabalhar nos Principios Mathematicos e a acompanhar alguns antigos alunos da Casa Pia que estudavam na Academia Real da Marinha. Em 1785–1786 envolveu-se em duas polémicas, com Monteiro da Rocha e com Garção Stockler (1759–1829), matemático e militar, em cartas que circularam mais ou menos publicamente. Nelas criticou ferozmente o rumo do ensino da matemática em Portugal e o nível científico da Academia das Ciências de Lisboa. Censurou também o estilo pouco rigoroso como muita matemática do século XVIII se apresentava; em particular, criticou o “fiel algebrista” Euler, colocando-se do lado do seu rival d’Alembert (um dos seus grandes heróis matemáticos, juntamente com Newton).
Foi só depois da sua morte, com 42 anos, em casa de João Paulo Bezerra de Seixas (amigo dos tempos de Valença e Coimbra), que as obras de José Anastácio da Cunha começaram a ser verdadeiramente publicadas.
Em 1790 apareceram os Principios Mathematicos, que tinham começado a ser impressos oito anos antes e que devem corresponder a uma evolução do antigo plano começado em 1766: uma obra onde fosse apresentada a base de toda a matemática, organizada tão logicamente quanto possível, seguindo o exemplo do rigor dos geómetras gregos antigos. Num pequeno volume de cerca de 300 páginas, dividido em 21 “livros”, Anastácio da Cunha vai da geometria elementar até ao cálculo de variações, passando pela aritmética, álgebra (resolução de equações), geometria analítica, cálculo diferencial e integral e cálculo de diferenças finitas. O estilo, além de extremamente conciso, é normalmente sintético, em vez de analítico: isto é, em vez de os resultados serem deduzidos, são enunciados e a seguir demonstrados. São de realçar três contributos originais nesta obra, que deram a Anastácio da Cunha a reputação internacional que tem tido nas últimas décadas.
Em primeiro lugar, o livro IX começa por definir “série convergente” como uma série tal que “venha a ser indifferente o continua-la ou naõ, por se poder desprezar sem erro notavel a somma de quantos termos se quizesse ajuntar aos já escritos ou indicados”. Tendo em conta a forma como esta definição é efetivamente usada nalgumas demonstrações deste livro, entende‑se que corresponde perfeitamente a dizer (em linguagem anacrónica) que uma série é convergente se a sucessão das suas somas parciais for o que se chama atualmente uma sucessão de Cauchy. Esta ideia, não como definição de convergência, mas como condição equivalente (estamos nos números reais) ou critério de convergência, viria a ser central nos trabalhos de Bolzano (1817) e Cauchy (década de 1820). Mas no século XVIII a convergência de séries era frequentemente um conceito vago, por vezes tratado contraditoriamente por um mesmo autor e aparentemente de importância secundária — quando era importante, era-o por motivos muito práticos de aproximação numérica. A atenção dada por Anastácio da Cunha a esta questão era, assim, muito invulgar e a sua solução ainda mais.
O livro IX prossegue com o tema do texto Logarithms & powers, referido acima, tratado de forma muito revista, mais direta e bastante mais sintética: a potência ab é definida como o número onde c é o número tal que
(isto é,
mas neste ponto o logaritmo ainda não está definido); assim, o expoente b pode ser positivo ou negativo, inteiro, fracionário ou irracional. A existência desse número c é verificada (para a positivo), assim como a convergência destas séries, são demonstradas as regras da aritmética das potências e o teorema binomial (expansão em série de
com
ou n positivo) e finalmente o logaritmo é definido como a inversa da exponencial.
O terceiro contributo é original apenas na forma publicada: no livro XV, Anastácio da Cunha trata o cálculo fluxionário essencialmente da mesma forma que tinha feito no manuscrito discutido acima, incluindo nomeadamente a sua definição analítica de fluxão.
Em 1807, D. Domingos de Sousa Coutinho, embaixador em Londres, fez publicar nessa cidade o Ensayo sobre os Principios de Mechanica, a partir de um manuscrito cuja data de composição se desconhece. Neste texto fica esboçado (mas apenas esboçado) um desenvolvimento axiomático da mecânica. Numa discussão preliminar, entre outras reflexões, encontramos mais uma originalidade (para a época). Anastácio da Cunha critica as tentativas de demonstração matemática dos princípios fundamentais da física, comuns entre os defensores do carácter necessário desses princípios; mas não se limita a defender a sua contingência, estabelecendo uma distinção crucial entre tratados de mecânica puramente matemáticos e tratados físico‑matemáticos: nos segundos os princípios fundamentais devem ser leis demonstradas experimentalmente (só o que se segue é que é matemático); enquanto o autor de um tratado puramente matemático, comparável ao autor de uma novela, a um pintor ou a um poeta, pode supor os princípios que quiser (por exemplo, “que a luz se propaga […] em linha circular”), pois “a verdade Mathematica naõ consiste senaõ na legitimidade, com que os theoremas, e as soluçoens dos problemas se derivam das definiçoens, postulados, e axiomas”. Naturalmente, “o Geometra, que naõ quizer incorrer na censura de inutil, deve tomar por principios […] verdades de facto, que a natureza, que a experiencia ensinam”. Esta liberdade radical concedida (em princípio) ao matemático, o carácter arbitrário dos axiomas e postulados, é no mínimo muito incomum no século XVIII, antes da geometria não‑euclidiana.
Em 1811, foi publicada em Bordéus uma tradução francesa dos Principios Mathematicos feita pelo seu amigo João Manuel d’Abreu. Este, que poderá ter conhecido Anastácio da Cunha em Valença, donde era natural, foi condenado pela Inquisição no mesmo auto‑de‑fé de 1778 e foi depois seu colega (professor de Matemática) na Casa Pia. Mais tarde entrou na Universidade de Coimbra, formando‑se em matemática em 1787. A tradução tem algumas incorreções, a principal das quais na definição de série convergente, tornando‑a falaciosa; mas foi a principal responsável por alguma (ainda que pouca) repercussão internacional de Anastácio da Cunha — incluindo a redescoberta historiográfica a partir da década de 1970.
Estas publicações foram promovidas por amigos de Anastácio da Cunha. As publicações de inéditos seus continuaram mais tarde, mas com propósitos mais historiográficos, à medida que foram sendo descobertos: a Carta Fisico-Mathematica em 1839, o Ensaio sobre as Minas em 1994 e vários manuscritos no Arquivo Distrital de Braga em 2006.
A obra poética e literária de Anastácio da Cunha também só foi publicada postumamente, tendo sido coligida por Inocêncio Francisco da Silva (1839), Hernâni Cidade (1930) e Maria Luísa Malato Borralho e Cristina Alexandra de Marinho (2001–2006).
João Caramalho Domingues
Centro de Matemática da Universidade do Minho
Arquivos
Lisboa, Arquivo Nacional da Torre do Tombo, Tribunal do Santo Ofício, Inquisição de Coimbra, proc. 8087 (Processo de José Anastácio da Cunha na Inquisição de Coimbra), PT/TT/TSO-IC/025/08087. (Transcrição publicada em O Processo de José Anastácio da Cunha na Inquisição de Coimbra (1778), introdução, transcrição e notas de João Pedro Ferro, Lisboa: Palas Editores, 1987.)
Braga, Arquivo Distrital de Braga / Universidade do Minho, Arquivo do Conde da Barca e Secção de Manuscritos. (Vários manuscritos científicos apógrafos de José Anastácio da Cunha, que foram publicados em Ensaio sobre as Minas e José Anastácio da Cunha. O Tempo, as Ideias, a Obra e… Os Inéditos, vol. 2 – v. referências abaixo.)
Vila Real, Arquivo da Fundação da Casa de Mateus, Secção 07 – D. José Maria de Sousa, 5º Morgado de Mateus (1758-1825). (Algumas dezenas de documentos matemáticos autógrafos de José Anastácio da Cunha; uma biografia composta por D. José Maria de Sousa, publicada como Anecdotas de J. A. d. C. – v. referência abaixo.)
Principios Mathematicos para instrucção dos alumnos do Collegio de Saõ Lucas, da Real Casa Pia do Castello de Saõ Jorge, Lisboa: Antonio Rodrigues Galhardo, 1790
Principes mathématiques de feu Joseph-Anastase da Cunha, traduits littéralement du portugais par J. M. D’Abreu, Bordéus: André Racle, 1811; 2.ª ed., Paris: Courcier, 1816
Ensayo sobre os Principios de Mechanica, publicado por D. D[omingos] A[ntónio] de S[ousa] C[outinho], Londres: J. Budd, 1807; 2.ª ed. em O Instituto, vol. 4 (1856), 212–214, 222–223, 236–238; 3.ª ed. em Anastácio da Cunha 1744/1787o matemático e o poeta (Lisboa: INCM, 1990), 339–351
Carta Fisico-Mathematica sobre a Theorica da Polvora em Geral, e a determinação do melhor comprimento das peças em particular; escrita por José Anastasio da Cunha em 1769, publicada por José Vitorino Damásio e Diogo Kopke, Porto: Typographia Commercial Portuense, 1838
Ensaio sobre as Minas, leitura, introdução e notas de Maria Fernanda Estrada, Braga: Arquivo Distrital de Braga, Universidade do Minho, 1994
Obra Literária, ed. Maria Luísa Malato Borralho e Cristina Alexandra de Marinho, Porto: Campo das Letras, 2 vols., 2001, 2006
José Anastácio da Cunha. O Tempo, as Ideias, a Obra e… Os Inéditos, vol. 2 (Os Inéditos), org. Maria Elfrida Ralha, Maria Fernanda Estrada, Maria do Céu Silva, Abel Rodrigues, Braga: Arquivo Distrital de Braga, Centro de Matemática da Universidade do Minho, Centro de Matemática da Universidade do Porto, 2006
Bibliografia sobre o biografado
Ferraz, Maria de Lurdes, Rodrigues, José Francisco, e Saraiva, Luís (org.), Anastácio da Cunha 1744/1787 o matemático e o poeta (Actas dum colóquio internacional e antologia de textos). Lisboa: INCM, 1990
Ralha, Maria Elfrida, Estrada, Maria Fernanda, Silva, Maria do Céu, e Rodrigues, Abel (org.), José Anastácio da Cunha. O Tempo, as Ideias, a Obra e… Os Inéditos, vol. 1 (O Tempo, as Ideias, a Obra), Braga: Arquivo Distrital de Braga, Centro de Matemática da Universidade do Minho, Centro de Matemática da Universidade do Porto, 2006
Rodrigues Abel, Duarte, António Leal, Ralha, Maria Elfrida, Malato, Maria Luísa (org.), Anecdotas de J. A. d. C. —Reminiscências de D. José Maria de Sousa, Morgado de Mateus, sobre o Mestre e Amigo José Anastácio da Cunha, V. N. Famalicão: Húmus, 2013
Universidade de Évora, Bicentenário da morte de Anastácio da Cunha — matemático e poeta, Évora, 1988
Youschkevitch, A. P. “J. A. da Cunha et les fondements de l’analyse infinitésimale”. Revue d’histoire des sciences 26 (1973): 3–22.
