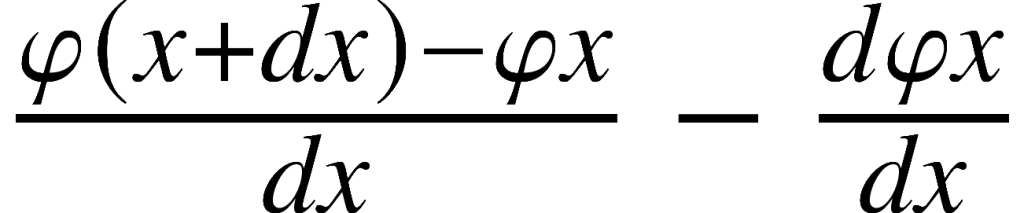Tag: Reforma Pombalina

Rocha, José Monteiro da

Canavazes, 25 junho 1734 – Lisboa, 11 dezembro 1819

Palavras-chave: Reforma Pombalina, Universidade de Coimbra, Observatório Astronómico, Matemática e ciências afins.

DOI: https://doi.org/10.58277/IFKO6192

José Monteiro da Rocha foi um dos principais responsáveis pela ampla e decisiva renovação de estudos no campo do ensino da matemática, da astronomia e das ciências naturais e experimentais operada pela Reforma Pombalina da Universidade de Coimbra. A sua obra científica é relativamente vasta, compreendendo traduções de livros de texto franceses, trabalhos de matemática aplicada e de astronomia José Monteiro da Rocha, filho primogénito de um casal de agricultores, Maria e João Teixeira, nasceu em 25 de junho de 1734, em Canavazes, uma pequena localidade perto de Marco de Canavezes. Conhece-se pouco sobre a sua infância e juventude. Com a idade de 18 anos partiu para o Brasil já como membro da Companhia de Jesus, onde entrou a 15 de outubro de 1752. Os poucos anos passados na Companhia foram vividos em São Salvador da Baía, no Colégio de Todos os Santos. Aí terá estudado humanidades e filosofia com Jerónimo Moniz (1723-?) e ciências com o alemão João Brewer. A sua sólida formação inicial adquirida no seio da Companhia revela-se desde logo nos seus trabalhos de juventude, dos quais, o Systema Physico Mathematico dos Cometas [1759-60]’ e o ‘Método de achar a longitude geográfica [1765-66]’ são exemplos paradigmáticos.

O primeiro é um texto de cariz didático, escrito aquando do tão esperado regresso do cometa Halley, com o objetivo de instruir o leitor nas noções básicas do cálculo astronómico e reforçar a verdadeira conceção da natureza celeste destes corpos (ironicamente não reconhece que as observações que faz, entre 13 de março e finais de abril de 1759, são na realidade do cometa Halley). Neste trabalho Monteiro da Rocha revela-se um newtoniano convicto, possuidor de uma sólida formação técnica. O ‘Método de achar a longitude’ é também ele paradigmático da sua formação, sobressaindo, desde logo, um conhecimento profundo e um domínio técnico e científico da questão da determinação da longitude no mar, que na altura (1759-65) era o centro de um importante debate no seio da comunidade astronómica e náutica internacional. Sendo um texto dedicado sobretudo aos marinheiros, cujo domínio matemático era muito reduzido, são constantes o cuidado e a clareza no discurso, sendo explicitados conceitos técnicos e matemáticos presentes no método das distâncias lunares, mas ainda ignorados na prática da navegação. Esta vertente didático-pedagógica de Monteiro da Rocha é uma característica que o acompanhará ao longo de toda a sua obra.

Após a expulsão dos Jesuítas, Monteiro da Rocha optou pela secularização e foi como professor público de Gramática Latina e Retórica que viveu a meia dúzia de anos que antecederam a sua vinda para Lisboa em 1766. Logo no ano seguinte matriculou-se na Universidade de Coimbra no curso de ânones, obtendo o grau de Bacharel três anos mais tarde, a 25 de junho de 1770. Foi neste período que travou amizade com Francisco de Lemos , o futuro reitor reformador da Universidade. Uma amizade que o levaria em 1771 a participar nos trabalhos da Junta de Providência Literária, um organismo criado por Pombal em 1770, para a Reforma da Universidade de Coimbra e do qual Francisco de Lemos fazia parte. A Reforma da Universidade pretendia ser a concretização de um projeto que tinha por finalidade sintonizar Portugal com as ideias do iluminismo europeu e encaminhá-lo na direção do progresso e das ciências. Pretendia-se, entre outras coisas, construir uma nova universidade aberta às ciências naturais e ao método experimental, em que todas as matérias estudadas fossem ‘iluminadas’ pela luz da razão. A universidade, colocada nas mãos do Estado, seria uma ferramenta insubstituível e indispensável para a desejada edificação de uma sociedade moderna, movida pela ciência e pelo progresso tecnológico. A ideologia e programa dos Estatutos (1772) para as ciências estão em perfeita sintonia com as ideias de D’Alembert , bem como de outros autores franceses seus condiscípulos, das quais os Estatutos mostram ser herdeiros. A matemática é um exemplo paradigmático do esforço racionalista subjacente a este projeto reformista. Recordemos que a cadeira de geometria (cadeira do 1º ano da Faculdade de Matemática) era comum a todos os cursos das várias faculdades.

O papel desempenhado por Monteiro da Rocha na reforma pombalina foi marcado por duas fases que, embora distintas, estão estreitamente ligadas. Uma diz respeito à elaboração dos Estatutos, e a outra é respeitante aos compêndios adotados. Monteiro da Rocha foi um dos principais responsáveis pela conceção e elaboração dos estatutos das novas ‘faculdades scientificas’, principalmente pela estruturação do ‘curso mathematico’ e definição do seu plano curricular e conteúdos programáticos. O ‘curso mathematico’ foi constituído em sete cadeiras: 1º ano, Geometria (+ Filosofia Racional e Moral + História Natural); 2º ano, Álgebra (+ Física Experimental); 3º ano, Foronomia (Física-Matemática); 4º ano, Astronomia. Havia ainda uma cadeira anexa de Desenho e Arquitetura a ser frequentada no 3º ou 4º ano. No que respeita aos compêndios para o ensino das diversas matérias – dos dez livros adotados, sete foram traduzidos para português, sendo Monteiro da Rocha responsável pela tradução de seis.

No início das aulas, em setembro de 1772, Monteiro da Rocha foi integrado na Faculdade de Matemática como professor de foronomia, cabendo-lhe a honra de ler a lição inaugural. Como os Estatutos reconheciam que para a docência só estavam habilitados aqueles que possuíssem grau de doutor, este foi-lhe concedido, assim como aos outros professores da faculdade, em 9 de outubro de 1772. O papel de Monteiro da Rocha na vida letiva e administrativa da faculdade e da universidade foi desde os primeiros tempos relevante.O seu empenho na prossecução do ideal universitário pombalino evidencia-se no modo como participou quer no domínio institucional, quer no científico e letivo. Primeiro como professor da cadeira de Foronomia (1772-83) e mais tarde como professor da cadeira de Astronomia (1783-1804), bem como diretor e decano da Faculdade de Matemática e diretor perpétuo do Observatório Astronómico da Universidade de Coimbra (OUAC, carta régia de 4 de abril de 1795). A ele se devem o projeto, a construção, a regulamentação e o apetrechamento instrumental do Observatório, que viria a ser inaugurado em 1799. A sua contribuição no que diz respeito à astronomia é bem mais vasta que a sua contribuição matemática. Essa contribuição que será fundamental para a futura atividade científica do próprio OAUC é ainda reforçada com o exercício da sua função de professor, que faz dele o principal responsável pela formação científica dos futuros astrónomos portugueses da primeira metade do século XIX.

No que diz respeito aos seus trabalhos matemáticos destacam-se dois manuscritos (s.d.), um de aritmética e outro de álgebra. O de aritmética tem por título ‘Elementos de Mathematica’ e divide-se em duas partes: para além da aritmética propriamente dita (intitulada de ‘Elementos de Arithmetica’) é iniciado com uns ‘Prolegómenos’, onde Monteiro da Rocha dá a entender que pretende ensinar outras matérias para além da aritmética. O facto do manuscrito de álgebra se intitular ‘Elementos de Álgebra’ e estar estruturado e organizado de modo semelhante ao de aritmética sugere a intenção da sua integração numa única obra. Hoje desconhecidos, mas referenciados entre os seus papéis pessoais haveria ainda uns ‘Elementos de geometria e trigonometria’ e um maço dedicado ao cálculo infinitesimal que, juntamente com os anteriores, fariam parte de um suposto compêndio de matemática que Monteiro da Rocha terá escrito por meados da década de 1760.

Por volta de 1786 Monteiro da Rocha escreveu um trabalho sobre o problema das quadraturas (integração), que seria publicado apenas em 1797 no 1º volume das Memórias da Academia das Ciências de Lisboa (ACL). Escrito em resposta aos comentários negativos feitos pelo seu ex-colega José Anastácio da Cunha a um trabalho de Manuel Coelho da Maia, premiado pela ACL em 1785, sobre a demonstração da regra de quadraturas (integração) de Fontaine . Comentários que se estendem ao próprio Monteiro da Rocha, gerando uma famosa ‘polémica’ que foi muito para além da questão matemática, originando uma severa troca de acusações de carácter pessoal de parte a parte, gerando partidários de ambos a assumirem severas posições adversárias. Nesse trabalho Monteiro da Rocha propôs dois métodos de aceleração da convergência, antecipando um método que Richardson proporá cerca de 130 anos mais tarde (em 1910) e que ficará conhecido na análise numérica como o método de extrapolação de Richardson. Ainda nesse 1º volume das Memórias da ACL Monteiro da Rocha publicou um outro trabalho sobre o cálculo de volumes. A ‘Solução geral do problema de Kepler sobre a medição das pipas e toneis’, assim se intitula, reflete bem a sua preocupação com a dimensão prática da matemática e a sua aplicabilidade na resolução de problemas concretos, ao pretender dar solução a um problema real no quotidiano do comércio de substâncias líquidas que se faziam transportar em pipas e tonéis; o de saber o volume parcial de líquido aí contido. Monteiro da Rocha elabora uma tabela que permite aos comerciantes estimar com precisão o volume parcial de uma pipa sabendo apenas os seus diâmetros maior, menor e médio, bem como o seu comprimento e a altura do líquido nela contido.

São vários os trabalhos de astronomia teórica e prática que Monteiro da Rocha publicou, grande parte deles escritos enquanto professor da cadeira de Astronomia (1783-1804) e diretor do Observatório (1795-1819). Estes trabalhos serão fundamentais para o estabelecimento dos métodos matemáticos e das práticas astronómicas que permitiram o cálculo e a elaboração das emblemáticas ‘Ephemerides Astronomicas’ que o Observatório Astronómico começou a publicar a partir de 1803.

O Observatório Astronómico da Universidade de Coimbra (OAUC), cuja concretização efetiva foi essencialmente da responsabilidade de Monteiro da Rocha, não se reduz apenas a um observatório de cariz universitário, direcionado exclusivamente para a vertente letiva. O papel e a prática astronómica que se requeriam para este estabelecimento (traçada desde logo nos Estatutos de 1772 e depois reforçada no regulamento de 1799) prende-o a uma dicotomia muito própria: por um lado como observatório universitário, nomeadamente no ensino prático da astronomia e na investigação científica dos seus professores e, por outro, como observatório nacional envolvendo-o na elaboração das efemérides astronómicas «para uso da Navegação Portuguesa». A criação do OAUC foi fundamental, na segunda metade do século XVIII, para a institucionalização da ciência astronómica em Portugal, durante o período em que a astronomia, sustentada pelos grandes avanços teóricos da mecânica celeste e da matemática aplicada, tenta, por fim, resolver as grandes questões que desde Newton (1643-1727) vinha enfrentando. Estas questões, ligadas aos problemas de navegação, geodesia e cartografia, determinação de órbitas de planetas e cometas, medições de tempo, e que faziam parte do programa de trabalho de qualquer observatório da época, estão também na base da criação e planificação do OAUC. A construção do Observatório esteve inicialmente planeada para o sítio do Castelo da cidade de Coimbra. A construção deste vasto equipamento iniciou-se em Abril de 1773, com as obras a pararem definitivamente em 1775 por dificuldades financeiras, quando estava realizado o essencial do primeiro piso. Entretanto edificou-se (c.1775), no terreiro do Paço das Escolas, para suprir as necessidades letivas, um pequeno observatório interino. Este observatório de carácter temporário acabaria por funcionar provisoriamente durante cerca de quinze anos, pois só em meados da década de 1780 se encarava definitivamente o problema da inexistência de um verdadeiro observatório astronómico conforme os Estatutos haviam estabelecido. Foi através da estreita colaboração entre Monteiro da Rocha (na qualidade de professor de astronomia e vice-reitor da Universidade) e Manuel Alves Macomboa (?-1815), o arquiteto da universidade, que surgiria o projeto definitivo para o OAUC, que aprovado pela universidade em 5 de fevereiro de 1791, se vê concluído em 1799. Os primeiros instrumentos, provenientes do Colégio dos Nobres, já haviam chegado de Lisboa logo no final de 1772. Ao longo dos anos seguintes Monteiro da Rocha encarregou-se de encomendar de França e Inglaterra muitos outros, estando praticamente reunido o núcleo principal dos instrumentos, nos meados da década de 1780. Após a sua inauguração em 1799, a atividade científica, da inteira responsabilidade de Monteiro da Rocha, centra-se no cálculo e na publicação das ‘Ephemerides Astronomicas’ (EAOAUC). O ponto sétimo do ‘Regulamento do Real Observatório Astronómico da Universidade de Coimbra’ (carta régia de 4 de dezembro de 1799) precisa bem o objetivo maior de toda a sua atividade científica: a elaboração de umas efemérides astronómicas, “para uso dele, [e que] igualmente possa servir para uso da Navegação Portuguesa”.

As EAOAUC serão a imagem de marca do trabalho astronómico do OAUC durante todo o século XIX. O primeiro volume foi publicado em 1803, pela Real Imprensa da Universidade, com as efemérides para o ano de 1804 e salvo dois períodos relativamente curtos em que a sua publicação esteve suspensa, as EAOAUC ainda eram publicadas no século XX. Para além das efemérides propriamente ditas, e à semelhança das congéneres estrangeiras, também as EAOAUC publicaram artigos científicos. Ao contrário das efemérides estrangeiras que calculavam diretamente partir das tabelas astronómicas as posições da Lua tanto para o meio-dia como para a meia-noite, as de Coimbra calculavam apenas o lugar do meio-dia diretamente das tabelas, sendo o lugar da meia-noite calculado por interpolação segundo um método proposto por Monteiro da Rocha, que vem publicado no volume 5, “Exposição dos Methodos Particulares de que se faz uso no cálculo destas Ephemerides” (1807). Em 1813 Monteiro da Rocha publicou as suas próprias tabelas astronómicas, ‘Taboas Astronómicas ordenadas a facilitar o Calculo das Ephemerides da Universidade de Coimbra’ (1813), que passaram a constituir a base de cálculo das EAOAUC até aos inícios da década de 1840.

A necessidade da elaboração e publicação por parte dos observatórios de efemérides astronómicas está intimamente ligada ao problema da determinação das longitudes geográficas, principalmente no alto mar, o que constituiu um dos maiores desafios enfrentados pela náutica e pela astronomia do século XVIII e inícios do século XIX. Monteiro da Rocha tem três trabalhos específicos, realizados em dois períodos distintos da sua vida, sobre o problema da determinação das longitudes. O já mencionado ‘Método de achar a longitude geográfica no mar e na terra’, nunca publicado, e escrito ainda antes da Reforma Pombalina da Universidade; os outros dois são a ‘Taboada Nautica para o calculo das Longitudes’ (1799) e o ‘Calculo das Longitudes’ (1803), escritos e publicados nos inícios do século XIX, quando o seu trabalho académico e científico já era reconhecido. Monteiro da Rocha publicou ainda nas EAOAUC três artigos sobre o cálculo dos eclipses e trânsitos de Mercúrio e Vénus: ‘Cálculo dos Eclipses’ (1803), ‘Demonstração e ampliação do cálculo dos eclipses’ (1806) e ‘Aditamento ao cálculo dos eclipses’ (1811).

Ainda no campo da astronomia teórica merece destaque o seu trabalho sobre a ‘Determinação das orbitas dos Cometas [1782]’ (1799). Com este trabalho, lido em 1782 em assembleia académica da ACL de Lisboa mas só publicado em 1799, Monteiro da Rocha perdeu a oportunidade de ficar inscrito na história da Astronomia como o primeiro a propor um método simples e de fácil aplicação na resolução de um dos problemas mais intrincados com que se debateu a astronomia do século XVIII: a determinação de órbitas de cometas. Perdeu essa primazia para o alemão Olbers (1758-1840), que em 1797 publicou um método muito parecido.

No campo da astronomia prática são relevantes dois trabalhos (também publicados nas EAOAUC), um sobre o ‘Uso do Instrumento das Passagens’ (1805), e outro sobre o ‘Uso do retículo romboidal’ (1805). Estes trabalhos, elogiosamente referidos por Delambre no Connaissance des Tems para o ano de 1810 (1808), contextualizados no conjunto da considerável obra astronómica de José Monteiro da Rocha, refletem a dicotomia e a excelência do astrónomo que era, tanto a nível teórico como prático.

No campo administrativo a ação de Monteiro da Rocha foi também variada e marcante, principalmente no trabalho que desempenhou como Vice-Reitor da Universidade (1786-1804). Monteiro da Rocha foi responsável por uma série de textos de carácter legislativo que ultrapassam em muito o estrito carácter académico. Dentre os mais significativos destacam-se o ‘Regulamento do Real Observatório Astronómico’, que é importante não só por estabelecer a lei orgânica do Observatório mas também porque nele se estabelece a necessidade de enviar professores da Universidade em viagens científicas ao estrangeiro para atualização de conhecimentos. Será em consequência desta lei que Manuel Pedro de Melo , professor da cadeira de Hidráulica, viajará, com instruções específicas redigidas por Monteiro da Rocha, para França e outros países europeus. Desse conjunto de leis merece igualmente destaque o ‘Regimento da Junta da Diretoria Geral dos Estudos’ (aviso régio de 10 de maio de 1800), organismo criado com a incumbência de fiscalizar a instrução pública e que veio substituir o Tribunal da Real Mesa da Comissão Geral sobre os Exames e Censura dos Livros. Refiram-se ainda a ‘Lei dos Cosmógrafos’ (alvará régio de 9 de junho de 1801), que introduziu uma profunda reforma na administração do território, instituindo em cada uma das comarcas do País um matemático com o título de ‘Cosmógrafo’ a reportar diretamente à administração central do Estado; e também o importante alvará de 1 de dezembro de 1804, que estabelecia o concurso como forma de provimento das cadeiras universitárias. Em 16 de Janeiro de 1780 Monteiro da Rocha foi eleito membro da ACL, vindo a ocupar alguns anos depois o cargo de diretor da classe das Ciências Exatas. Em 1798 Monteiro da Rocha seria eleito membro da Sociedade Real Marítima, Militar e Geográfica (criada em 30 de junho desse ano), e em 1799 eleito vogal da Junta da Diretoria Geral de Estudos e Escolas do Reino. Em 21 de Março de 1800 Monteiro da Rocha tornou-se conselheiro do Príncipe Regente D. João. No ano seguinte, em 2 de Junho de 1801, recebeu a Comenda da Ordem de Cristo da Sé de Portalegre, como reconhecimento dos seus serviços. Ainda no tempo do Marquês de Pombal, pelos mesmos motivos, havia sido nomeado para uma cadeira magistral da Sé de Leiria (18 de fevereiro de 1774) e em 1779 designado para o cargo de principal do Real Colégio dos Nobres das três Províncias do Norte. Em 1804, devido à nomeação para preceptor do príncipe herdeiro, futuro rei D. Pedro IV, e de seus irmãos (carta régia de 18 de agosto de 1804), Monteiro da Rocha abandonou a vida universitária ativa, passando a residir em São José de Ribamar, em Lisboa. Monteiro da Rocha morreu em 11 de Dezembro de 1819.

Fernando B. Figueiredo
Universidade de Coimbra

Arquivos

Processo Académico de José Monteiro da Rocha, Lisboa, Academia das Ciências de Lisboa

Processo do Professor José Monteiro da Rocha, Coimbra, Arquivo da Universidade de Coimbra, AUC Cx. 265

Obras

‘Segunda Parte. Do Curso Mathematico’. 1772. In Estatutos da Universidade de Coimbra. II Centenário da Reforma Pombalina. Por Ordem da Universidade de Coimbra. 3: 141-222. Coimbra

“Additamentos à regra de M. Fontaine para resolver por approximação os Problemas que se reduzem às Quadraturas”. 1797. Memórias da Academia Real das Sciencias de Lisboa, I: 218-243

“Solução Geral do problema de Kepler sobre a medição das Pipas e Tonéis.” 1797. Memórias da Academia Real das Sciencias de Lisboa, I: 1-36

“Determinação das órbitas dos Cometas”. 1799. Memórias da Academia Real das Sciencias de Lisboa, II: 402-479

Taboada Nautica para o calculo das Longitudes, por José Monteiro da Rocha da Universidade de Coimbra em 14 de Março de 1799. [1801]. Lisboa: Typographia Chalcografica, e Litteraria do Arco do Cego

Ephemerides Astronomicas calculadas para o Meridiano do Observatorio da Universidade de Coimbra para o uso do mesmo Observatório, e para o da navegação Portugueza [EAOAUC]. Coimbra: Real Imprensa da Universidade (são vários volumes, o 1º é de 1803)

“Taboas Auxiliares”. 1803-1804. EAOAUC 1: 121-170; 2: 121-165

“Cálculo das Longitudes”. 1803. EAOAUC 1 : 213-230

Mémoires sur l’Astronomie Pratique par M. J. Monteiro da Rocha. 1808. Paris: Courcier

Taboas Astronomicas ordenadas a facilitar o cálculo das Ephemerides da Universidade de Coimbra. 1813. Coimbra: Imprensa da Universidade

Bibliografia sobre o biografado

Teixeira, António José. 1888-1890. “Cartas do Dr. José Monteiro da Rocha a D. Francisco de Lemos de Faria Pereira Coutinho.” O Instituto: Jornal scientifico e litterario 36 (1888-1889) 305-310, 372-376, 449-454, 509-514, 587-593, 657-663, 732-736, 793-798; 37 (1889-1890) 53-57, 128-132, 197-204, 268-275, 338-340, 475-479, 560-564, 622-628, 709-714, 799-804, 881-884

Teixeira, António José. 1889-1889. “Sciencias moraes e sociaes. Apontamentos para a biographia de José Monteiro da Rocha.” O Instituto: Jornal scientifico e litterario 37: 65-98

Teixeira, Francisco Gomes. 1925. Panegíricos e Conferências. Coimbra: Imprensa da Universidade

Figueiredo, Fernando B. 2005. “A contribuição de José Monteiro da Rocha para o cálculo da órbita de cometas.” Tese de Mestrado, FCT-UNL

Figueiredo, Fernando B. 2011. “José Monteiro da Rocha e a actividade científica da ‘Faculdade de Mathematica’ e do ‘Real Observatório da Universidade de Coimbra’: 1772-1820.” Tese de Doutoramento, FCTUC

Sobral, Thomé Rodrigues

Felgueiras, Torre de Moncorvo, 21 dezembro 1759 — Coimbra, 20 setembro 1829

Palavras-chave: Reforma Pombalina, Universidade Coimbra, Laboratório Químico.

DOI: https://doi.org/10.58277/EHSH3302

Filho de João Rodrigues e de Isabel Pires, Thomé Rodrigues Sobral nasceu em Felgueiras, Torre de Moncorvo, a 21 de dezembro de 1759, e morreu a 20 de setembro de 1829, em Coimbra. Matriculou-se nas Faculdades de Matemática e de Filosofia da Universidade de Coimbra, em outubro de 1779. Em 1782, foi ordenado presbítero em Braga, e, em 1783, formou-se em matemática e filosofia. Em 1786, foi nomeado demonstrador de história natural; e lente-substituto de física, em 1786-1788; de história natural, em 1787: e de química, em 1789.

Em 1791, Rodrigues Sobral foi nomeado professor da cadeira de Química e Metalurgia, sucedendo a Domingos Vandelli. Nesta data, assumiu também o cargo de director do Laboratório Químico da Universidade de Coimbra.

Como refere Joaquim Augusto Simões de Carvalho (1822-1902) na sua Memória Histórica da Faculdade de Filosofia(Imprensa da Universidade, Coimbra,1882), “no tempo da direcção deste Professor, os trabalhos práticos do Laboratório não cessavam, não só em delicadas investigações de química, mas ainda nas mais importantes aplicações industrais” .

Foi sócio da Academia das Ciências de Lisboa e cavaleiro professo da Ordem de Cristo.

Em julho de 1791, a congregação da Faculdade de Filosofia atribuiu a Rodrigues Sobral a tarefa de escrever um compêndio de química, decidindo também que o artigo Affinité da autoria de Guyton de Morveau, publicado na Encyclopédie Méthodique, deveria ser traduzido para português. O reitor incumbiu o demonstrador da cadeira de química,Vicente de Seabra , de o fazer, mas, inesperadamente, Rodrigues Sobral viria a fazer a tradução, apresentando-a, em 1793, com o título Tractado das Affinidades Chimicas, artigo que no Diccionario de Chimica, fazendo parte da Encyclopedia por ordem de materias, deu Mr. De Morveau, com um longo prefácio de sua autoria, com considerações sobre a necessidade do estudo da química para o avanço dos países e também sobre as novas orientações desta disciplina.

Quanto ao compêndio de química, em 25 de Abril de 1792, Rodrigues Sobral submeteu à congregação a primeira parte do plano do mesmo e, em Julho desse mesmo ano, as restantes partes. Em meados de 1798, como o compêndio ainda não estivesse pronto, Rodrigues Sobral foi libertado da docência no ano lectivo de 1798/1799 de modo a facilitar-lhe otrabalho. Entretanto, a Universidade adoptou o compêndio baseado na teoria do flogisto da autoria de Scopoli, intitulado Fundamenta Chemiae-Praelectionibus Publicis Accomodata. (Praga, Wolfgangum Gerlb, 1777).

Aparentemente, Rodrigues Sobral não era um adepto do flogisto. O naturalista alemão Heinrich F. Link, que visitou Portugal nessa altura, refere que ele estava a par dos desenvolvimentos recentes da química francesa, nomeadamente, da teoria do oxigénio da Lavoisier, e ele próprio o deixou claro no referido prefácio que fez para o Tractado das Affinidades Chimicas. A redacção final e completa do compêndio de química de que fora incumbido é desconhecida e, se alguma vezfoi concluída, não há notícia de que tenha sido publicado. Entretanto, o ensino da química, em Coimbra, mudou em 1801, com a divisão da cadeira de Química e Metalurgia em duas disciplinas distintas, o que poderá ter levado Rodrigues Sobral a considerar que o seu conteúdo já não corresponderia cabalmente às necessidades da cadeira para que o elaborara, evitando publicá-lo. Na sua falta e após longa discussão sobre o assunto, em 1807, a congregação decidiu adoptar os Elementa Chemiae Universae et Medicae-Praelectionibus suis Accomodata (Coimbra, Typis academicis, 1807) de J. F. AJacquin.

Em 1807, os exércitos de Napoleão sob o comando do general J. A. Junot atacaram Coimbra. Rodrigues Sobral tornou-se então responsável pela produção de pólvora em larga escala, no laboratório químico da Universidade. A sua acção foi elogiada pelos oficiais britânicos, aliados dos portugueses contra os invasores, que lhe deram o título de «mestre da pólvora». As tropas francesas retaliaram, incendiando a casa em que Rodrigues Sobral vivia, nos arredores da cidade. No incêndio, o «mestre da pólvora», perdeu a sua biblioteca, e com ela, as suas notas de investigações e o manuscrito do seu compêndio de química.

Nos anos que se seguiram à passagem das tropas de Napoleão por Coimbra, Rodrigues Sobral empenhou-se completamente em tornar o laboratório químico de grande utilidade para a Nação; de interesse para a Universidade; de crédito e consideração para as outras Nações.

Logo em 1809, com a região de Coimbra devastada pela peste, Rodrigues Sobral ocupou-se por completo na orientação e execução de várias medidas de desinfeção, nomeadamente, as fumigações com ácido muriático, em aquartelamentos, hospitais e outros locais e edifícios públicos, servindo-lhe de mestre, nos procedimentos adotados, como ele próprio oreconheceu, o químico francês Guyton de Morveau. Depois ocupou-se da análise química de exemplares de quinas recebidas do Brasil, assim como de variadas minas metálicas que lhe chegavam, para o efeito, de diversos pontos do país, e também de várias águas minerais. Escreveu sobre diversos assuntos de química, nomeadamente sobre análise química, granjeando a consideração geral dos seus pares a ponto de ser considerado «o melhor e mais autorizado químico portuguêsda altura».

Em 1816, Sobral anunciou que estava a preparar uma memória sobre nomenclatura química portuguesa, a qual também nunca viria a ser publicada, apesar de ter recebido o estímulo e a aprovação da Congregação da Faculdade de Filosofia, em 24 de julho de 1824. Por volta de 1820, Sobral iniciou a sua atividade política, no quadro da Revolução Liberal de 1820, tendo entrado no circuito de cargos e mordomias que não lhe deixavam muito tempo para a investigação química. Foi eleito deputado em 1821.

Afastado de Coimbra entre 1821 e 1822, Sobral interrompeu a atividade docente, participou numa comissão encarregada da reforma da Faculdade de Filosofia, e, em 1825, foi nomeado para uma comissão destinada a avaliar as reformas da agricultura portuguesa, proposta pela Academia das Ciências, a mando do governo. Em 24 de Maio de 1828, Rodrigues Sobral foi nomeado vice-reitor da Universidade de Coimbra, mas devido a problemas de saúde, teve dedeclinar o cargo.

António M. Amorim da Costa
Departamento de Química, Universidade de Coimbra

Arquivo

Coimbra, Arquivo da Biblioteca Geral da Universidade

Obras

Sobral, Tomé Rodrigues (trad.), “Tractado das Affinidades Chimicas, artigo que no Diccionario de Chimica, fazendo parte da Encyclopedia por ordem de materias, deu Mr. de Morveau” Coimbra: Real Imprensa da Universidade, 1793.

Sobral, Tomé Rodrigues, “Diário das operações, que se fizerão em Coimbra, a fim de se atalharem os progressos do contágio em Agosto de 1809” J. de Coimbra, 5 (1813): 103-138.

Sobral, Tomé Rodrigues, “Ensaio Chimico da planta chamada no Brasil ‘mil homens’, Aristolochia Grandiflora, segundo o Dr. Bernardino António Gomes “ J. de Coimbra, 7 (1814): 149-198.

Sobral, Tomé Rodrigues , “Carta ao Doutor José Feliciano de Castilho em resposta a outras, em que se tratava de huma nova applicação do Gaz Muriático oxigenado (Gaz oximuriatico)” J. de Coimbra, 7 (1814): 101-136.

Sobral, Tomé Rodrigues, “Oratio Pro Solemni Studiorum Annuaque de More Instauratione Habui” J. de Coimbra, 7 (1814): 67-85.

Sobral, Tomé Rodrigues, “Reflexões geraes sobre as difficuldades de uma boa analyse principalmente vegetal” J. de Coimbra, 7 (1814): 251-266.

Sobral, Tomé Rodrigues, “Sobre os trabalhos em grande que no laboratório chimico da Universidade poderão praticar-se com mais utilidade do Público, e com maiores vantagens do mesmo Estabelecimento” J. de Coimbra, 9 (1816): 293-312.

Sobral, Tomé Rodrigues, “Notícia de differentes Minas Metallicas e Salinas” J. de Coimbra, 9 (1816): 221-240.

Sobral, Tomé Rodrigues, “Observações sobre um Escrito, intitulado Methodo prático de purificar as cartas e papéis procedentes de paizes contagiados ou suspeitosos”J. de Coimbra, 11 (1817): 101-130.

Sobral, Tomé Rodrigues, “Memória sôbre o Principio Febrifugo das Quinas” J. de Coimbra, 15 (1819): 126-153.

Bibliografia sobre o biografado

Amorim da Costa, António. “Thomé Rodrigues Sobral (1759-1829). A Química ao serviço da Comunidade” Publicações do II Centenário da Academia das Ciências de Lisboa, 2 (1986), 373-401

Amorim da Costa, António “A Universidade de Coimbra na Vanguarda da Química do Oxigénio” Publicações do II Centenário da Academia das Ciências de Lisboa, 2 (1986), 403-416

Amorim da Costa, António. Primórdios da Ciência Química em Portugal. (Instituto Camões, Biblioteca Breve, Lisboa, 1984).

Cunha, José Anastácio da

José Anastácio da Cunha (Lisboa, 1744 – 1 de janeiro de 1787)

Palavras-chave: matemático, livre-pensador, poeta.

DOI: https://doi.org/10.58277/KNIH4583

José Anastácio da Cunha foi um dos primeiros professores da Faculdade de Matemática criada na reforma pombalina da Universidade de Coimbra. A sua obra, publicada postumamente, revela uma preocupação invulgar para a época com o rigor lógico, e particularmente com definições precisas e gerais. Algumas das suas definições são frequentemente vistas como precursoras de soluções adotadas a partir do século XIX.

José Anastácio da Cunha nasceu numa família modesta, mas não sem algumas ligações importantes. O seu pai, Lourenço da Cunha, foi um pintor conceituado, autor de cenários teatrais e de algumas pinturas em igrejas e capelas, e foi juiz da Irmandade de São Lucas (corporação de pintores e artistas). A sua mãe, Jacinta Inês, foi criada na casa do tesoureiro-mor do reino.

Com o pai, Anastácio da Cunha aprendeu desenho, incluindo perspetiva e talvez um pouco de geometria, mas fez os estudos formais na escola da Congregação do Oratório no Convento das Necessidades, à parte uma passagem de dois anos pela Universidade de Coimbra para cursar Leis, sem seguimento.

Em 1764 foi nomeado primeiro-tenente do Regimento de Artilharia do Porto, aquartelado em Valença. Aí travou amizade com diversos oficiais estrangeiros ao serviço do exército português. Aprendeu inglês e possivelmente alemão (em Lisboa já tinha aprendido latim e francês). O convívio com estrangeiros, muitos deles heréticos do ponto de vista católico da época, influenciou profundamente Anastácio da Cunha, que se tornou um livre-pensador. Leu e traduziu autores como Pope, Voltaire e Shakespeare, além de compor poesia própria. Um dos estrangeiros com quem conviveu foi o capitão inglês Richard Muller, filho de John Muller, professor da Royal Military Academy de Woolwich e autor de vários compêndios de matemática, artilharia e fortificação. Muller e mais tarde o coronel escocês James Ferrier, deram a Anastácio da Cunha acesso a alguma da mais importante bibliografia científica britânica, incluindo os Principia Mathematica e outras obras de Newton. As primeiras produções científicas conhecidas de Anastácio da Cunha datam desta fase e relacionam-se com aplicações militares: o Ensaio sobre as Minas, não datado (mas anterior a março de 1768) e a Carta Físico-Matemática sobre a Teórica da Pólvora em Geral e a determinação do melhor comprimento das peças em particular, de 1769. No entanto, segundo declarações posteriores à Inquisição, começou também em 1766 a trabalhar numa obra com «a Baze de toda a Mathematica»; é provável que essa obra corresponda à Arithmetica Universal de que se sabe que existia uma versão em 1771.

Em 1773 José Anastácio da Cunha foi nomeado pelo marquês de Pombal lente de Geometria na Universidade de Coimbra, completando o quadro docente da Faculdade de Matemática (FM) criada na reforma pombalina da instituição. No ano anterior tinham sido nomeados os outros três lentes: os italianos Miguel Franzini e Miguel António Ciera e o ex-jesuíta português José Monteiro da Rocha. Geometria era o título da cadeira do primeiro ano, que compreendia aritmética, geometria (sintética) e trigonometria plana. Em Coimbra, Anastácio da Cunha parece ter direcionado a sua atenção mais para a matemática pura. Em abril de 1776, propôs na Congregação da FM, sem sucesso, a adoção duns Elementos de Geometria que tinha composto “por metodo mais breve e mais facil”.

Ainda em Coimbra compôs um texto em inglês: Logarithms & powers, datado de maio de 1778, uma investigação sobre um tema que lhe era caro — a maneira correta de definir potências e logaritmos, de forma a abarcar todos os casos dos expoentes (naturais, fracionários e irracionais) logo na definição. No século XVIII as potências eram definidas como multiplicações repetidas, o que só faz sentido com expoentes naturais; potências de expoentes fracionários e irracionais eram calculadas utilizando expressões cuja validade estava demonstrada apenas para expoentes naturais. Uma situação semelhante acontecia com as definições de logaritmos. Anastácio da Cunha era extremamente crítico deste tipo de abordagem, em que as definições não cobrem todos os casos. A sua proposta naquele texto consistia em definir os logaritmos a partir de uma equação funcional (a soma dos logaritmos é igual ao logaritmo do produto) e depois definir e estudar a exponencial como função inversa do logaritmo. Tecnicamente recorria à série de potências da exponencial, depois de verificar que a sua função inversa verifica a equação funcional dos logaritmos.

Em Coimbra, travou amizade com alguns jovens estudantes nobres que viriam a fazer parte duma elite política e cultural, particularmente na regência de D. João. Entre eles contavam‑se D. Rodrigo de Sousa Coutinho (futuro diplomata e secretário de estado em várias pastas), D. Domingos de Sousa Coutinho (futuro diplomata) e D. José Maria de Sousa (também futuro diplomata, o mais conhecido dos morgados de Mateus; é célebre a sua edição dos Lusíadas). Quanto aos seus colegas da FM, parece ter tido boas relações com Ciera, mas um pouco mais tensas com Franzini e Monteiro da Rocha, que viriam a ter posições de maior influência (o primeiro foi mestre dos príncipes D. José e D. João e o segundo Vice-Reitor da Universidade e figura importante na Academia das Ciências de Lisboa).

Em julho de 1778, cerca de um ano e meio após a morte de D. José e o afastamento do marquês de Pombal (isto é, em plena Viradeira), José Anastácio da Cunha foi preso pela Inquisição. Considerado culpado de heresia e apostasia, por ter caído nos erros do deísmo, tolerantismo e indiferentismo, foi condenado a confisco de todos os seus bens, três anos de reclusão na Congregação do Oratório em Lisboa (Casa das Necessidades), quatro anos de degredo em Évora e proibição de voltar a entrar em Coimbra ou Valença. Posteriormente foi-lhe comutado um ano de reclusão e perdoado o degredo em Évora.

Durante os dois anos de reclusão Anastácio da Cunha manteve atividade científica. Escreveu pelo menos um texto sobre balística e uma versão dos Princípios do Cálculo Fluxionário, sobre outro dos seus temas importantes: a fundamentação do cálculo diferencial (a que chamava “fluxionário”, usando terminologia newtoniana). Ao longo do século XVIII houve muitas discussões sobre como fundamentar o cálculo diferencial; uma das duas respostas mais importantes recorria a quantidades infinitamente pequenas ou infinitésimos (Leibniz) e a outra argumentava com limites (Newton e d’Alembert); mas as quantidades infinitamente pequenas não pareciam bem definidas (ora se comportavam como zeros, ora não) e os argumentos com limites eram vagos. A proposta de Anastácio da Cunha consistia resumidamente em substituir as quantidades infinitésimas por variáveis infinitésimas — variáveis que podiam tomar valores arbitrariamente pequenos, mas não infinitamente pequenos — e em definir fluxão de φx como a grandeza dφx que, supondo dx infinitésimo, fizer dφx/dx constante e

infinitésimo ou zero. Esta definição foi descrita por diversos historiadores desde a década de 1970 como a primeira definição analítica rigorosa de diferencial.

Nos finais de 1779, foi fundada a Academia das Ciências de Lisboa, instalada precisamente no edifício oratoriano das Necessidades onde Anastácio da Cunha estava recluso. Este nunca pertenceu à Academia, mas foi consultado, através do padre oratoriano Teodoro de Almeida, seu amigo e diretor espiritual, e também académico fundador, a propósito de problemas de matemática a propor pela Academia.

Depois de libertado, Anastácio da Cunha tentou publicar, por subscrição, uns Ensaios Mathematicos em dois volumes, que seriam uma compilação de estudos seus, revistos, sobre temas de matemática pura (geometria, “aritmética universal”, cálculo fluxionário) e mecânica. O anúncio na Gazeta de Lisboa (15/6/1781) resumia a preocupação científica fundamental de Anastácio da Cunha: “remover, e destruir muitas das grandes difficuldades, que ainda hoje fazem assás precaria a evidencia de algumas partes da Mathematica […] conservar a evidencia, rigor, e elegancia dos Geometras Gregos”. Contudo, o número de subscritores foi insuficiente para a publicação.

Por essa altura, mas em data que não é possível precisar, o intendente-geral da Polícia, Pina Manique, convidou José Anastácio da Cunha para regente (ou inspetor) dos estudos e substituto das cadeiras de matemática no colégio da Casa Pia de Lisboa, recém-criada. Nessa qualidade, Anastácio da Cunha elaborou o Plano de Estudos do colégio. Alguns dos seus alunos na Casa Pia viriam a ter carreiras académicas: Manuel Pedro de Melo foi professor na FM de Coimbra, tendo ganhado em 1806 um prémio da Academia Real de Copenhaga; Tristão Álvares da Costa Silveira foi professor na Academia dos Guardas-Marinhas e depois na FM de Coimbra. Também com o patrocínio de Pina Manique começaram a imprimir-se os seus Principios Mathematicos, provavelmente em 1782. Segundo João Manuel d’Abreu, à medida que eram impressos, os primeiros cadernos deste livro eram utilizados no ensino no colégio, sob supervisão de Anastácio da Cunha. O lugar de Anastácio da Cunha na Casa Pia não durou muito tempo, mas também não se sabe exatamente quando terminou. Em 1783, ainda constava na folha de vencimentos da Casa Pia, mas em 1785 queixava-se de terem destruído a obra do intendente.

Nos dois ou três últimos anos da sua vida José Anastácio da Cunha, para além de não ter emprego, sofreu de problemas de saúde, tendo de recorrer à ajuda de amigos. Continuou a trabalhar nos Principios Mathematicos e a acompanhar alguns antigos alunos da Casa Pia que estudavam na Academia Real da Marinha. Em 1785–1786 envolveu-se em duas polémicas, com Monteiro da Rocha e com Garção Stockler (1759–1829), matemático e militar, em cartas que circularam mais ou menos publicamente. Nelas criticou ferozmente o rumo do ensino da matemática em Portugal e o nível científico da Academia das Ciências de Lisboa. Censurou também o estilo pouco rigoroso como muita matemática do século XVIII se apresentava; em particular, criticou o “fiel algebrista” Euler, colocando-se do lado do seu rival d’Alembert (um dos seus grandes heróis matemáticos, juntamente com Newton).

Foi só depois da sua morte, com 42 anos, em casa de João Paulo Bezerra de Seixas (amigo dos tempos de Valença e Coimbra), que as obras de José Anastácio da Cunha começaram a ser verdadeiramente publicadas.

Em 1790 apareceram os Principios Mathematicos, que tinham começado a ser impressos oito anos antes e que devem corresponder a uma evolução do antigo plano começado em 1766: uma obra onde fosse apresentada a base de toda a matemática, organizada tão logicamente quanto possível, seguindo o exemplo do rigor dos geómetras gregos antigos. Num pequeno volume de cerca de 300 páginas, dividido em 21 “livros”, Anastácio da Cunha vai da geometria elementar até ao cálculo de variações, passando pela aritmética, álgebra (resolução de equações), geometria analítica, cálculo diferencial e integral e cálculo de diferenças finitas. O estilo, além de extremamente conciso, é normalmente sintético, em vez de analítico: isto é, em vez de os resultados serem deduzidos, são enunciados e a seguir demonstrados. São de realçar três contributos originais nesta obra, que deram a Anastácio da Cunha a reputação internacional que tem tido nas últimas décadas.

Em primeiro lugar, o livro IX começa por definir “série convergente” como uma série tal que “venha a ser indifferente o continua-la ou naõ, por se poder desprezar sem erro notavel a somma de quantos termos se quizesse ajuntar aos já escritos ou indicados”. Tendo em conta a forma como esta definição é efetivamente usada nalgumas demonstrações deste livro, entende‑se que corresponde perfeitamente a dizer (em linguagem anacrónica) que uma série é convergente se a sucessão das suas somas parciais for o que se chama atualmente uma sucessão de Cauchy. Esta ideia, não como definição de convergência, mas como condição equivalente (estamos nos números reais) ou critério de convergência, viria a ser central nos trabalhos de Bolzano (1817) e Cauchy (década de 1820). Mas no século XVIII a convergência de séries era frequentemente um conceito vago, por vezes tratado contraditoriamente por um mesmo autor e aparentemente de importância secundária — quando era importante, era-o por motivos muito práticos de aproximação numérica. A atenção dada por Anastácio da Cunha a esta questão era, assim, muito invulgar e a sua solução ainda mais.

O livro IX prossegue com o tema do texto Logarithms & powers, referido acima, tratado de forma muito revista, mais direta e bastante mais sintética: a potência a^b é definida como o número onde c é o número tal que (isto é, mas neste ponto o logaritmo ainda não está definido); assim, o expoente b pode ser positivo ou negativo, inteiro, fracionário ou irracional. A existência desse número c é verificada (para a positivo), assim como a convergência destas séries, são demonstradas as regras da aritmética das potências e o teorema binomial (expansão em série decomou n positivo) e finalmente o logaritmo é definido como a inversa da exponencial.

O terceiro contributo é original apenas na forma publicada: no livro XV, Anastácio da Cunha trata o cálculo fluxionário essencialmente da mesma forma que tinha feito no manuscrito discutido acima, incluindo nomeadamente a sua definição analítica de fluxão.

Em 1807, D. Domingos de Sousa Coutinho, embaixador em Londres, fez publicar nessa cidade o Ensayo sobre os Principios de Mechanica, a partir de um manuscrito cuja data de composição se desconhece. Neste texto fica esboçado (mas apenas esboçado) um desenvolvimento axiomático da mecânica. Numa discussão preliminar, entre outras reflexões, encontramos mais uma originalidade (para a época). Anastácio da Cunha critica as tentativas de demonstração matemática dos princípios fundamentais da física, comuns entre os defensores do carácter necessário desses princípios; mas não se limita a defender a sua contingência, estabelecendo uma distinção crucial entre tratados de mecânica puramente matemáticos e tratados físico‑matemáticos: nos segundos os princípios fundamentais devem ser leis demonstradas experimentalmente (só o que se segue é que é matemático); enquanto o autor de um tratado puramente matemático, comparável ao autor de uma novela, a um pintor ou a um poeta, pode supor os princípios que quiser (por exemplo, “que a luz se propaga […] em linha circular”), pois “a verdade Mathematica naõ consiste senaõ na legitimidade, com que os theoremas, e as soluçoens dos problemas se derivam das definiçoens, postulados, e axiomas”. Naturalmente, “o Geometra, que naõ quizer incorrer na censura de inutil, deve tomar por principios […] verdades de facto, que a natureza, que a experiencia ensinam”. Esta liberdade radical concedida (em princípio) ao matemático, o carácter arbitrário dos axiomas e postulados, é no mínimo muito incomum no século XVIII, antes da geometria não‑euclidiana.

Em 1811, foi publicada em Bordéus uma tradução francesa dos Principios Mathematicos feita pelo seu amigo João Manuel d’Abreu. Este, que poderá ter conhecido Anastácio da Cunha em Valença, donde era natural, foi condenado pela Inquisição no mesmo auto‑de‑fé de 1778 e foi depois seu colega (professor de Matemática) na Casa Pia. Mais tarde entrou na Universidade de Coimbra, formando‑se em matemática em 1787. A tradução tem algumas incorreções, a principal das quais na definição de série convergente, tornando‑a falaciosa; mas foi a principal responsável por alguma (ainda que pouca) repercussão internacional de Anastácio da Cunha — incluindo a redescoberta historiográfica a partir da década de 1970.

Estas publicações foram promovidas por amigos de Anastácio da Cunha. As publicações de inéditos seus continuaram mais tarde, mas com propósitos mais historiográficos, à medida que foram sendo descobertos: a Carta Fisico-Mathematica em 1839, o Ensaio sobre as Minas em 1994 e vários manuscritos no Arquivo Distrital de Braga em 2006.

A obra poética e literária de Anastácio da Cunha também só foi publicada postumamente, tendo sido coligida por Inocêncio Francisco da Silva (1839), Hernâni Cidade (1930) e Maria Luísa Malato Borralho e Cristina Alexandra de Marinho (2001–2006).

João Caramalho Domingues
Centro de Matemática da Universidade do Minho

Arquivos

Lisboa, Arquivo Nacional da Torre do Tombo, Tribunal do Santo Ofício, Inquisição de Coimbra, proc. 8087 (Processo de José Anastácio da Cunha na Inquisição de Coimbra), PT/TT/TSO-IC/025/08087. (Transcrição publicada em O Processo de José Anastácio da Cunha na Inquisição de Coimbra (1778), introdução, transcrição e notas de João Pedro Ferro, Lisboa: Palas Editores, 1987.)

Braga, Arquivo Distrital de Braga / Universidade do Minho, Arquivo do Conde da Barca e Secção de Manuscritos. (Vários manuscritos científicos apógrafos de José Anastácio da Cunha, que foram publicados em Ensaio sobre as Minas e José Anastácio da Cunha. O Tempo, as Ideias, a Obra e… Os Inéditos, vol. 2 – v. referências abaixo.)

Vila Real, Arquivo da Fundação da Casa de Mateus, Secção 07 – D. José Maria de Sousa, 5º Morgado de Mateus (1758-1825). (Algumas dezenas de documentos matemáticos autógrafos de José Anastácio da Cunha; uma biografia composta por D. José Maria de Sousa, publicada como Anecdotas de J. A. d. C. – v. referência abaixo.)

Principios Mathematicos para instrucção dos alumnos do Collegio de Saõ Lucas, da Real Casa Pia do Castello de Saõ Jorge, Lisboa: Antonio Rodrigues Galhardo, 1790

Principes mathématiques de feu Joseph-Anastase da Cunha, traduits littéralement du portugais par J. M. D’Abreu, Bordéus: André Racle, 1811; 2.ª ed., Paris: Courcier, 1816

Ensayo sobre os Principios de Mechanica, publicado por D. D[omingos] A[ntónio] de S[ousa] C[outinho], Londres: J. Budd, 1807; 2.ª ed. em O Instituto, vol. 4 (1856), 212–214, 222–223, 236–238; 3.ª ed. em Anastácio da Cunha 1744/1787o matemático e o poeta (Lisboa: INCM, 1990), 339–351

Carta Fisico-Mathematica sobre a Theorica da Polvora em Geral, e a determinação do melhor comprimento das peças em particular; escrita por José Anastasio da Cunha em 1769, publicada por José Vitorino Damásio e Diogo Kopke, Porto: Typographia Commercial Portuense, 1838

Ensaio sobre as Minas, leitura, introdução e notas de Maria Fernanda Estrada, Braga: Arquivo Distrital de Braga, Universidade do Minho, 1994

Obra Literária, ed. Maria Luísa Malato Borralho e Cristina Alexandra de Marinho, Porto: Campo das Letras, 2 vols., 2001, 2006

José Anastácio da Cunha. O Tempo, as Ideias, a Obra e… Os Inéditos, vol. 2 (Os Inéditos), org. Maria Elfrida Ralha, Maria Fernanda Estrada, Maria do Céu Silva, Abel Rodrigues, Braga: Arquivo Distrital de Braga, Centro de Matemática da Universidade do Minho, Centro de Matemática da Universidade do Porto, 2006

Bibliografia sobre o biografado

Ferraz, Maria de Lurdes, Rodrigues, José Francisco, e Saraiva, Luís (org.), Anastácio da Cunha 1744/1787 o matemático e o poeta (Actas dum colóquio internacional e antologia de textos). Lisboa: INCM, 1990

Ralha, Maria Elfrida, Estrada, Maria Fernanda, Silva, Maria do Céu, e Rodrigues, Abel (org.), José Anastácio da Cunha. O Tempo, as Ideias, a Obra e… Os Inéditos, vol. 1 (O Tempo, as Ideias, a Obra), Braga: Arquivo Distrital de Braga, Centro de Matemática da Universidade do Minho, Centro de Matemática da Universidade do Porto, 2006

Rodrigues Abel, Duarte, António Leal, Ralha, Maria Elfrida, Malato, Maria Luísa (org.), Anecdotas de J. A. d. C. —Reminiscências de D. José Maria de Sousa, Morgado de Mateus, sobre o Mestre e Amigo José Anastácio da Cunha, V. N. Famalicão: Húmus, 2013

Universidade de Évora, Bicentenário da morte de Anastácio da Cunha — matemático e poeta, Évora, 1988

Youschkevitch, A. P. “J. A. da Cunha et les fondements de l’analyse infinitésimale”. Revue d’histoire des sciences 26 (1973): 3–22.